Scary Dark Energy and Einstein's Field Equations
Thought: Why are we discussing Einstein field equations and the various constants that are used in Einsteins work as it relates to Dark Energy? This is a website written by someone who does Machine Learning and Data Analysis???
Today we will discuss:
*The Einstein field equations are a set of partial differential equations that describe how the curvature of spacetime is related to the distribution of matter and energy in the universe.
*Dark energy is a form of energy that is thought to be responsible for the observed accelerating expansion of the universe. It is often modeled using a cosmological constant term in the Einstein field equations.
*The cosmological constant is a parameter introduced by Einstein to counterbalance the attractive force of gravity and is related to the energy density of the vacuum of space.
*A stress-energy tensor is a mathematical object describing the universe’s distribution of matter and energy. It appears on the right-hand side of the Einstein field equations.
*The Riemann curvature tensor is a mathematical object that describes the curvature of spacetime, and it appears on the left-hand side of the Einstein field equations.
*Solving the Einstein field equations can be difficult, especially for complex systems. However, the equations are a powerful tool for understanding the behavior of gravity in extreme environments, such as black holes and the early universe.
*Python and other programming languages can be used to model and visualize the behavior of dark energy and other cosmological phenomena, such as the universe’s expansion over time.
In 3 dimensions, the Einstein equation of general relativity can be written as:
\[G_{ij} = 8\pi T_{ij}\]where \(G_{ij}\) is the Einstein tensor and \(T_{ij}\) is the stress-energy tensor. The Einstein tensor can be written in terms of the Ricci tensor, \(R_{ij}\), and the Ricci scalar, \(R\), as:
\[G_{ij} = R_{ij} - \frac{1}{2}g_{ij}R\]where \(g_{ij}\) is the metric tensor. The Ricci tensor and scalar can be expressed in terms of the Christoffel symbols, \(\Gamma^i_{jk}\), and the partial derivatives of the metric, \(g_{ij,k}\), as:
\[R_{ij} = g^{kl}(\Gamma^i_{jk,l} - \Gamma^i_{jl,k} + \Gamma^m_{jk}\Gamma^i_{ml} - \Gamma^m_{jl}\Gamma^i_{mk})\] \[R = g^{ij}R_{ij}\]The Ricci tensor, denoted by \(R_{\mu\nu}\), is a mathematical object that arises in the study of general relativity, which is the theory of gravity developed by Albert Einstein in the early 20th century. The Ricci tensor is a contraction of the Riemann curvature tensor, which describes the curvature of spacetime in four dimensions.
The Ricci tensor is defined in terms of the Riemann curvature tensor \(R^{\rho}_{\ \ \mu \nu \sigma}\) by taking a contraction over one pair of indices:
\[R_{\mu\nu} = R^{\rho}_{\ \ \mu \rho \nu}\]The Ricci tensor is symmetric, meaning that \(R_{\mu\nu} = R_{\nu\mu}\). This symmetry arises because the Riemann curvature tensor is symmetric in its last two indices, \(R^{\rho}{\ \ \mu \nu \sigma} = R^{\rho}{\ \ \nu \mu \sigma}\), and the contraction over one pair of indices results in a symmetric object.
The Ricci tensor plays a fundamental role in the Einstein field equations, which are the equations that describe how matter and energy interact with spacetime to produce gravity. The field equations are written in the form:
\[R_{\mu\nu} - \frac{1}{2} g_{\mu\nu} R = 8\pi T_{\mu\nu}\]Here, \(g_{\mu\nu}\) is the metric tensor, which describes the geometry of spacetime, and \(T_{\mu\nu}\) is the stress-energy tensor, which represents the distribution of matter and energy in spacetime. The left-hand side of the equation involves the Ricci tensor and the scalar curvature \(R\), which is a contraction of the Riemann curvature tensor. The right-hand side of the equation involves the stress-energy tensor, which represents the matter and energy that produce the gravitational field.
The Einstein field equations are a set of partial differential equations that determine the geometry of spacetime in the presence of matter and energy. They are a cornerstone of modern theoretical physics. They have been used to make many predictions about the behavior of black holes, the evolution of the universe, and other astrophysical phenomena.
The stress-energy tensor describes the distribution of matter and energy in the universe and can be written as:
\[T_{ij} = \rho v_i v_j + p\delta_{ij}\]where \(\rho\) is the energy density, \(v_i\) is the velocity vector, \(p\) is the pressure, and \(\delta_{ij}\) is the Kronecker delta.
Where does the pressure term come from? This is space, after all. Is pressure a significant factor here? The presence of pressure in the stress-energy tensor is essential in describing the behavior of matter and energy in the universe, even without a medium such as air or water. In fact, pressure can significantly impact the dynamics of matter and energy in the vacuum of space, particularly on large scales such as those relevant to cosmology. In the context of the Einstein field equations, pressure appears in the stress-energy tensor due to the microscopic properties of the matter and energy that make up the universe. Pressure effects can often be neglected on small scales, such as those relevant for laboratory experiments, because they are small compared to other forces and energies. However, on cosmological scales, pressure can become a dominant force that affects the overall dynamics of the universe. For example, pressure in the stress-energy tensor can lead to the formation of cosmic structures, such as galaxies and clusters of galaxies. The pressure of the gas and dust that make up these structures can balance the gravitational attraction between the matter, leading to stable configurations. In addition, pressure can affect the dynamics of the early universe, when the universe was much hotter and denser than it is today. In this regime, pressure can help to prevent the universe from collapsing in on itself, and it can also drive the rapid expansion of the universe during a period known as inflation. Overall, the pressure term in the stress-energy tensor is an essential component of our understanding of the behavior of matter and energy in the universe. It plays a crucial role in many predictions and applications of general relativity and cosmology.
The Kronecker delta, denoted by \(\delta_{ij}\), is a mathematical symbol that takes the value one if its indices are equal and 0 otherwise. In other words:
\[\delta_{ij} = \begin{cases} 1, & \text{if } i=j \\ 0, & \text{if } i \neq j \end{cases}\]The Kronecker delta is a commonly used symbol in mathematics and physics, and it often appears in equations that involve summation or manipulation of indices. It is also frequently used in the context of tensors, where it is used to raise and lower indices or to contract indices in various ways.
For example, in the context of the stress-energy tensor, the Kronecker delta appears in the pressure term, which is often written as \(p\delta_{ij}\), where \(p\) is the pressure and \(i\) and \(j\) are indices denoting spatial coordinates. This term represents the pressure exerted by a fluid or gas in the \(i\)-th and \(j\)-th directions. The Kronecker delta ensures the pressure is isotropic (i.e., the same in all spatial directions).
The stress-energy tensor can also be written in terms of the energy-momentum tensor, \(T^{\mu\nu}\), as:
\[T_{ij} = T^0_0 \gamma_{ij} + T^i_j\]Where \(\gamma_{ij}\) is the spatial part of the metric tensor. The field equations can be derived by solving for the Einstein tensor in terms of the Ricci tensor and scalar and equating it to the stress-energy tensor. The resulting equation is \(G_{ij} = 8\pi T_{ij}\), which relates the curvature of spacetime to the distribution of matter and energy in the universe.
The Einstein field equations can be written as a set of ten partial differential equations, one for each component of the metric tensor \(g_{\mu\nu}\), which depends on four spacetime coordinates \(x^\mu = (x^0,x^1,x^2,x^3)\). The equations take the form:
\[R_{\mu\nu} - \frac{1}{2} g_{\mu\nu} R = 8\pi T_{\mu\nu}\]where \(R_{\mu\nu}\) is the Ricci tensor, \(R\) is the scalar curvature, and \(T_{\mu\nu}\) is the stress-energy tensor.
Expanding the Ricci tensor in terms of the Christoffel symbols \(\Gamma^\rho_{\mu\nu}\) and their derivatives, we have:
\[R_{\mu\nu} = \partial_\rho \Gamma^\rho_{\mu\nu} - \partial_\nu \Gamma^\rho_{\mu\rho} + \Gamma^\rho_{\mu\nu} \Gamma^\sigma_{\rho\sigma} - \Gamma^\rho_{\mu\sigma} \Gamma^\sigma_{\nu\rho}\]where the partial derivative \(\partial_\rho\) is with respect to the spacetime coordinate \(x^\rho\).
Substituting this expression into the Einstein field equations and simplifying, we obtain the following set of ten partial differential equations:
\(G_{00} = R_{00} - \frac{1}{2} g_{00} R = 8\pi T_{00}\) \(G_{01} = R_{01} - \frac{1}{2} g_{01} R = 8\pi T_{01}\) \(G_{02} = R_{02} - \frac{1}{2} g_{02} R = 8\pi T_{02}\) \(G_{03} = R_{03} - \frac{1}{2} g_{03} R = 8\pi T_{03}\) \(G_{11} = R_{11} - \frac{1}{2} g_{11} R = 8\pi T_{11}\) \(G_{12} = R_{12} - \frac{1}{2} g_{12} R = 8\pi T_{12}\) \(G_{13} = R_{13} - \frac{1}{2} g_{13} R = 8\pi T_{13}\) \(G_{22} = R_{22} - \frac{1}{2} g_{22} R = 8\pi T_{22}\) \(G_{23} = R_{23} - \frac{1}{2} g_{23} R = 8\pi T_{23}\) \(G_{33} = R_{33} - \frac{1}{2} g_{33} R = 8\pi T_{33}\)
These equations relate the curvature of spacetime, described by the Ricci tensor and scalar curvature, to the distribution of matter and energy in spacetime, represented by the stress-energy tensor. Solving the Einstein field equations is challenging and requires advanced mathematical techniques and numerical simulations. Still, the equations have led to many vital predictions and insights in modern theoretical physics.
The Riemann curvature tensor, denoted by \(R^\rho_{\ \ \mu\nu\sigma}\), is a mathematical object that describes the curvature of spacetime in four dimensions. It is a tensor with four indices and measures how much spacetime geometry deviates from Euclidean geometry, which is the geometry of flat space. The Riemann curvature tensor is defined in terms of the Christoffel symbols \(\Gamma^\rho_{\mu\nu}\), which are coefficients that describe the connection between neighboring points in a curved space. The Christoffel symbols are themselves defined in terms of the metric tensor \(g_{\mu\nu}\), which describes the geometry of spacetime as: \(\Gamma^\rho_{\mu\nu} = \frac{1}{2} g^{\rho\sigma} \left( \frac{\partial g_{\sigma\mu}}{\partial x^\nu} + \frac{\partial g_{\sigma\nu}}{\partial x^\mu} - \frac{\partial g_{\mu\nu}}{\partial x^\sigma} \right)\)
Where \(g^{\rho\sigma}\) are the components of the inverse metric tensor. The Riemann curvature tensor is then given by:
\[R^\rho_{\ \ \mu\nu\sigma} = \frac{\partial \Gamma^\rho_{\mu\sigma}}{\partial x^\nu} - \frac{\partial \Gamma^\rho_{\mu\nu}}{\partial x^\sigma} + \Gamma^\rho_{\lambda\sigma} \Gamma^\lambda_{\mu\nu} - \Gamma^\rho_{\lambda\nu} \Gamma^\lambda_{\mu\sigma}\]The Riemann curvature tensor measures the non-Euclidean nature of spacetime and encapsulates many critical features of general relativity. For example, the Riemann tensor is used to describe tidal forces, which arise when a massive object like a star or a black hole warps the geometry of spacetime around it. The Riemann tensor is also used to calculate the geodesic deviation equation, which describes how two initially parallel geodesics in spacetime will converge or diverge due to the curvature of spacetime.
The Riemann tensor is a fundamental object in general relativity and plays a central role in many of the theory’s most important predictions and applications. It is a challenging object to work with mathematically, but it is essential for understanding the geometry of spacetime and the behavior of matter and energy in curved space.
Dark energy is thought to be a form of energy that permeates all of space and is responsible for the observed acceleration of the universe’s expansion. Dark energy is typically represented by a cosmological constant term in the Einstein field equations context, denoted by \(\Lambda\).
The addition of the cosmological constant to the Einstein field equations modifies the right-hand side of the equation, which represents the distribution of matter and energy in spacetime. The modified field equations take the form:
\[R_{\mu\nu} - \frac{1}{2} g_{\mu\nu} R + \Lambda g_{\mu\nu} = 8\pi T_{\mu\nu}\]Here, the cosmological constant \(\Lambda\) is a constant of nature that represents the energy density of the vacuum of space. The cosmological constant term contributes to the stress-energy tensor in a way that mimics the effects of a fluid with negative pressure. This property is thought to be exhibited by dark energy. The presence of the cosmological constant term in the Einstein field equations has several important implications. First, it leads to a modification of how gravity behaves on large scales. Instead of the gravitational attraction between matter causing the expansion of the universe to slow down, as would be expected in the absence of dark energy, the presence of dark energy causes the expansion of the universe to accelerate. Second, the cosmological constant term contributes to the overall curvature of spacetime, which can have significant consequences for the structure and evolution of the universe. In particular, the value of the cosmological constant affects the ultimate fate of the universe and the size and shape of the universe on large scales. Finally, dark energy and the cosmological constant term in the Einstein field equations challenge our understanding of fundamental physics. The cosmological constant is thought to represent a form of vacuum energy that arises from the properties of empty space. Its presence in the universe raises questions about the nature of empty space and the quantum vacuum.
The quantum vacuum is a concept in quantum field theory that describes the state of space at the smallest scales. According to quantum field theory, space is not truly empty but contains a collection of constantly fluctuating and interacting quantum fields. The fields have a minimum energy level in the quantum vacuum, known as the ground state. This ground-state energy gives rise to a vacuum energy that permeates all of space. The vacuum energy is a fundamental property of nature that arises from the quantum properties of the fields, and it is thought to contribute to a variety of physical phenomena, including the cosmological constant term that appears in the Einstein field equations. The concept of the vacuum energy is intimately related to the uncertainty principle of quantum mechanics, which states that the more precisely the position of a particle is known, the less exactly its momentum can be known, and vice versa. This uncertainty principle implies that the vacuum is never truly empty but is instead filled with virtual particles that pop into and out of existence. These virtual particles arise from fluctuations in the quantum fields, and they can give rise to observable physical effects, such as the Casimir effect, which is the force that arises between two closely spaced plates in a vacuum. The concept of the quantum vacuum is a central feature of modern physics. It has important implications for our understanding of the behavior of matter and energy in the universe. The vacuum energy and the cosmological constant term that arise from it are thought to play a vital role in the universe’s accelerating expansion. They present a significant challenge to our current understanding of fundamental physics.
Several mathematical tools and equations describe the quantum vacuum in more detail. One of the most important is the vacuum expectation value, which measures the average value of a quantum field in the vacuum state. The vacuum expectation value is given by:
\[\langle 0 | \hat{\phi}(x) | 0 \rangle\]where \(\hat{\phi}(x)\) is the field operator, which describes the behavior of the quantum field at a point \(x\), and \(|0\rangle\) is the vacuum state of the field. The vacuum expectation value is a complex quantity that depends on the properties of the quantum field. It can calculate various physical quantities, such as the vacuum energy and the Casimir effect. Another crucial mathematical tool for describing the quantum vacuum is the renormalization procedure, a technique for dealing with infinities that arise in quantum field theory calculations. In quantum field theory, many physical quantities are calculated using perturbative techniques, which involve an infinite sum of terms. However, these sums often diverge, meaning they go to infinity, making them impossible to calculate. The renormalization procedure involves redefining specific parameters in the theory to cancel out the infinities, resulting in finite physical predictions. Finally, the mathematical framework of quantum field theory itself provides a powerful tool for understanding the behavior of the quantum vacuum. Quantum field theory is a mathematical framework that describes the behavior of quantum fields, including the quantum fields that make up the vacuum. By treating the vacuum as a quantum field, quantum field theory provides a rigorous and systematic way to calculate the properties of the vacuum, such as the vacuum energy and the Casimir effect.
Section 2
An example of how to solve one of the Einstein field equations. Let’s consider the case where the stress-energy tensor is that of a perfect fluid, which is given by:
\[T_{\mu\nu} = (\rho + P)u_\mu u_\nu + Pg_{\mu\nu}\]where \(\rho\) is the energy density of the fluid, \(P\) is its pressure, and \(u^\mu\) is the four-velocity of a fluid element. This approximation is useful for many astrophysical systems, such as stars and galaxies.
We can then consider the Einstein field equation:
\(G_{\mu\nu} = 8\pi T_{\mu\nu}\) Where \(G_{\mu\nu}\) is the Einstein tensor, a function of the metric tensor and its derivatives. For this example, let’s assume that we are interested in a spherically symmetric system, such as a star, and we use the Schwarzschild metric:
\(ds^2 = -f(r)dt^2 + \frac{1}{f(r)}dr^2 + r^2(d\theta^2 + \sin^2\theta d\phi^2)\) Where \(f(r)\) is a function of the radial coordinate \(r\) that depends on the mass and density of the star.
Using the spherical symmetry of the system, we can assume that the fluid velocity is purely radial, so \(u^\mu = (u^t, u^r, 0, 0) = (f(r)^{-1/2}, 0, 0, 0)\). We can also assume that the fluid is isotropic, so \(T_{\theta\theta} = T_{\phi\phi} = P\).
With these assumptions, we can write the Einstein field equation for the \(tt\) component as: \(G_{tt} = 8\pi T_{tt}\) Using the Schwarzschild metric and the stress-energy tensor for a perfect fluid, we can calculate the left-hand side of this equation:
\(G_{tt} = \frac{f''}{f} - \frac{f'}{2rf} + \frac{1-f}{r^2f}\) A prime denotes a derivative with respect to the radial coordinate \(r\). We can also calculate the right-hand side of the equation using the stress-energy tensor:
\(T_{tt} = \rho u_t u_t = \rho f^{-1}\) Substituting these expressions into the Einstein field equation, we get:
\(\frac{f''}{f} - \frac{f'}{2rf} + \frac{1-f}{r^2f} = 8\pi\rho f^{-1}\) This is a second-order ordinary differential equation for the function \(f(r)\), which can be solved numerically or analytically in some special cases. For example, in the case of a non-rotating, spherically symmetric star with a uniform density, the solution is the well-known Schwarzschild interior solution:
\(f(r) = 1 - \frac{8\pi}{3} G\rho r^2\) This solution describes the curvature of spacetime inside the star and can be used to calculate various physical quantities, such as the radius and mass of the star. This is one example of how Einstein field equations can be solved, and in general, the equations are challenging to solve precisely for more complicated systems. Nonetheless, they are a powerful tool for understanding the behavior of gravity in extreme environments, such as black holes and the early universe.
Here’s an example of how to use Matplotlib to plot the scale factor of the universe over time, as predicted by the Lambda-CDM cosmological model. The scale factor measures how the universe has expanded over time. It is related to the Hubble parameter, a key parameter in the Einstein field equations. The Lambda-CDM model predicts that the universe’s expansion is accelerating due to the presence of dark energy.
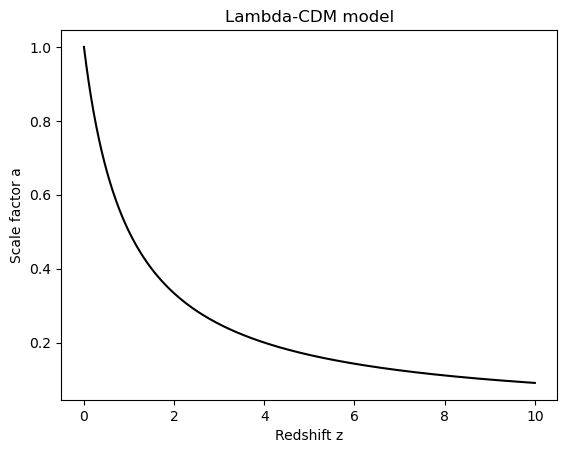
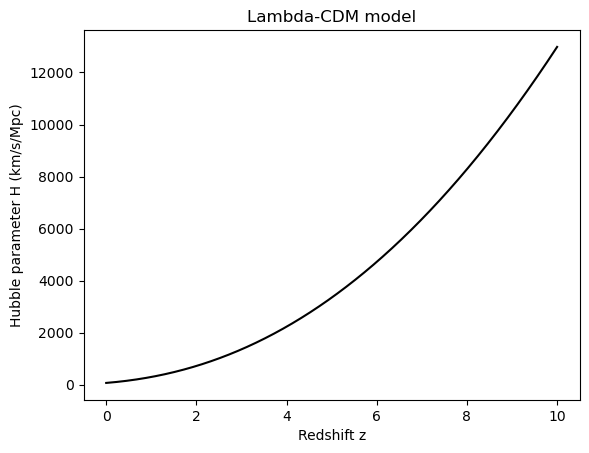
This code defines the parameters of the Lambda-CDM model and uses them to calculate the scale factor and Hubble parameter as a function of redshift. It then uses Matplotlib to create two plots: one of the scale factor as a function of redshift, and one of the Hubble parameters as a function of redshift. These plots show how the universe has expanded over time and how the expansion rate has changed due to the presence of dark energy.